There is a lot more proof behind a right triangle than you think.

“The Pythagorean Theorem is the statement that the sum of (the areas of) the two small squares equals the area of the big one” (Bogomolny, 2010). In algebraic terms, a² + b² = c² when c is the hypotenuse and a and b are the legs of the right triangle.
Hundreds of years have passed since Pythagoras proved his theorem. In the centuries since, many mathematicians have developed new proofs that support Pythagoras’ work. Below are three of the most concrete and viable proofs that support the infamous right triangle theorem. In addition to these explanations, there are more than sixty more proofs of the theorem here.
The key is to understand that in a right triangle, the two small sides squared equal the longest side squared.
"To the Pythagoreans number was a living thing - it was real, a substance of the landscape" (Pythagoras, 2010).
Hundreds of years have passed since Pythagoras proved his theorem. In the centuries since, many mathematicians have developed new proofs that support Pythagoras’ work. Below are three of the most concrete and viable proofs that support the infamous right triangle theorem. In addition to these explanations, there are more than sixty more proofs of the theorem here.
The key is to understand that in a right triangle, the two small sides squared equal the longest side squared.
"To the Pythagoreans number was a living thing - it was real, a substance of the landscape" (Pythagoras, 2010).
Euclid's Bride Chair
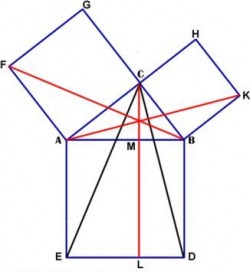
First of all, ΔABF = ΔAEC by SAS. This is because, AE = AB, AF = AC, and ∠BAF = ∠BAC + ∠CAF = ∠CAB + ∠BAE = ∠CAE
ΔABF has base AF and the altitude from B equal to AC. Its area equals half of the square on side AC. ΔAEC has AE and the altitude from C equal to AM, where M is the point of intersection of AB with the line CL parallel to AE. Here the area of ΔAEC equals half that of the rectangle AELM which concludes that the area AC² of the square on side AC equals the area of the rectangle AELM. Additionally, the area BC² of the square on side BC equals that of rectangle BMLD. The two rectangles AELM and BMLD make up the square on the hypotenuse AB (Bogomolny, 2010).
ΔABF has base AF and the altitude from B equal to AC. Its area equals half of the square on side AC. ΔAEC has AE and the altitude from C equal to AM, where M is the point of intersection of AB with the line CL parallel to AE. Here the area of ΔAEC equals half that of the rectangle AELM which concludes that the area AC² of the square on side AC equals the area of the rectangle AELM. Additionally, the area BC² of the square on side BC equals that of rectangle BMLD. The two rectangles AELM and BMLD make up the square on the hypotenuse AB (Bogomolny, 2010).
Another Proof Option
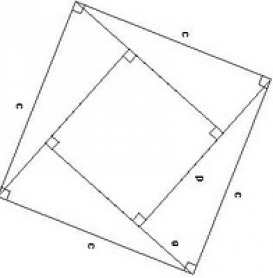
Begin with four copies of the same triangle. Three of these have been rotated 90°, 180°, and 270°, respectively. Each has area a times b divided by 2. Put them together without additional rotations so that they form a square with side c.
The formed square has a square hole with the side (a - b) in the center. Summing up its area (a - b)² and 2ab, the area of the four triangles (4·ab/2), simplifies to the equation below (Weisstein, n.d.).
c²= (a - b)² + 2ab
= a² - 2ab + b² + 2ab
= a² + b²
The formed square has a square hole with the side (a - b) in the center. Summing up its area (a - b)² and 2ab, the area of the four triangles (4·ab/2), simplifies to the equation below (Weisstein, n.d.).
c²= (a - b)² + 2ab
= a² - 2ab + b² + 2ab
= a² + b²
Proof Using Squares
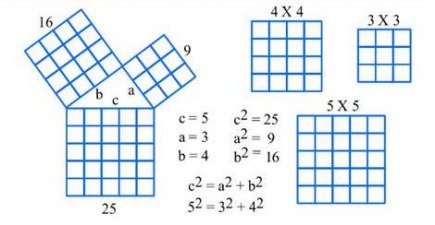
Creating three squares, one that totals 25 square units, one that totals 16 square units and one that totals 9 square units arrange them to create a central triangle ABC. Because squares are forming the triangle, it is also a right triangle.
The length of side a = 3, b = 4, and c = 5. When these values are squared according to Pythagoras' theorem we can conclude that 25 = 25.
The length of side a = 3, b = 4, and c = 5. When these values are squared according to Pythagoras' theorem we can conclude that 25 = 25.
